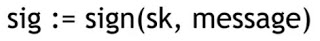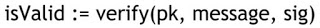区块链学习笔记(一)——加密货币简介
19 Jan 2018
本文是对 coursera 的 Bitcoin and Cryptocurrency Technologies课程笔记。
1.1 密码学中的哈希函数 (Cryptographic Hash function)
哈希函数三个一般特性:
-
输入为任意长度的字符串 (takes any string as input)
-
输出为固定长度 (fixed-size output)
固定长度可以设置为任意值。
比特币使用 256 位。
- 有效计算 (efficiently computable)
对于输入的字符串,能在合理的时间内计算出其输出。
跟安全相关的特性(Security Properties):
- 碰撞阻力 (collision free)
沒有人能找出 hash collision 的可能。Collision 肯定存在,也就是说,没有完美的哈希函数,在现实场景中,我们只需要保证“没有人能够通过计算来找到碰撞”。
在此前提下,对于确定的哈希函数,如果输出相同,则可以认为输入也相同。
应用场景:通过信息摘要进行大文件的对比。
- 隐蔽性 (hiding)
如果输入都来自一个比较小的集合,那他人几乎肯定可以通过枚举计算然后与输出对比的方式来确定输入,所以输入必须分散。
通过将不分散的输入与另外一个分散的输入结合而产生的输入,可以实现隐蔽性。比如说将输入扩大为 256 位的随机字符串
应用场景:承诺(Commitment)。将 msg 和随机的 key 输入进承诺函数(commit()),得到输出 commitment,并公布。在之后需要公布真正的 msg 时,只要将 key 一起公布,便可以验证之前公布的 msg。这个过程如同:将要公布的消息写下来提前放到信封中,然后在你公布信息之后,可以通过拆开信封来验证你公布的信息是否与之前一样。当然,为了避免被暴力破解,msg 需要与随机 key 结合后,进行一次哈希。
- 谜题友好 (puzzle-friendly)
可以理解为,具备该特性的哈希函数,只能穷举尝试输入来获得解,没有其他更好的策略。
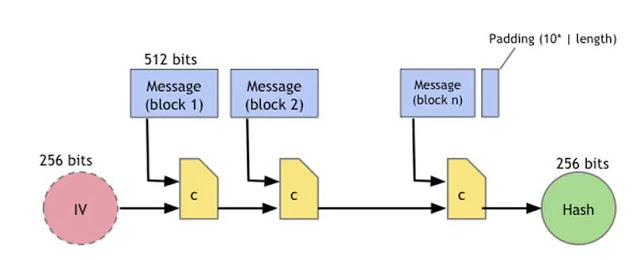
安全哈希算法 (Secure Hash Algorithm 256,简称 SHA-256)
比特币使用 SHA-256 进行加密。
上述过程大概为:首先将要加密的信息分割成 512 bit 的数据块(block),如果最后一个数据块不足 512 bit 则进行 Padding 补足,直到可被 512 整除。将 256 bit 的初始向量与第一个 512 bit 的数据块(一共 768 bit)输入到 c 函数中,得到 256 位的输出,然后再跟第二块数据块结合作为 c 函数的输入,一直循环到所有的数据块都处理完,得到的 256 bit 数据即为 SHA-256 的结果。
这里有个前提推论,具有碰撞阻力的 c 函数经过变换后生成的哈希函数也具有碰撞阻力。
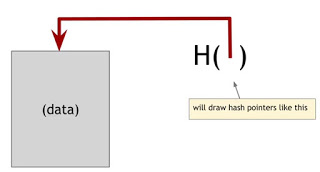
1.2 哈希指针和数据结构 (Hash Point and Data Structure)
哈希指针存储了数据存储的位置,以及数据的 hash 值。我们可以在找到数据的同时,通过 hash 值对其进行校验。
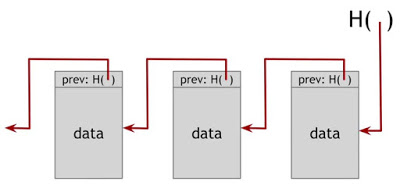
区块链 (Block chain)
使用哈希指针可以构建如下的数据结构:
上面的数据结构就可以称作区块链。每个元素使用哈希指针指向前一个元素。
当链中某一数据被篡改后,数据的哈希值也会改变,想要保证能够校验,则需要将元素后面的所有元素都修改,而且即便修改到最后一个元素,也没法修改我们所持有的最后的指针。
梅克尔树 (Merkle tree)
也可以使用指针创建二叉树,即梅克尔树。
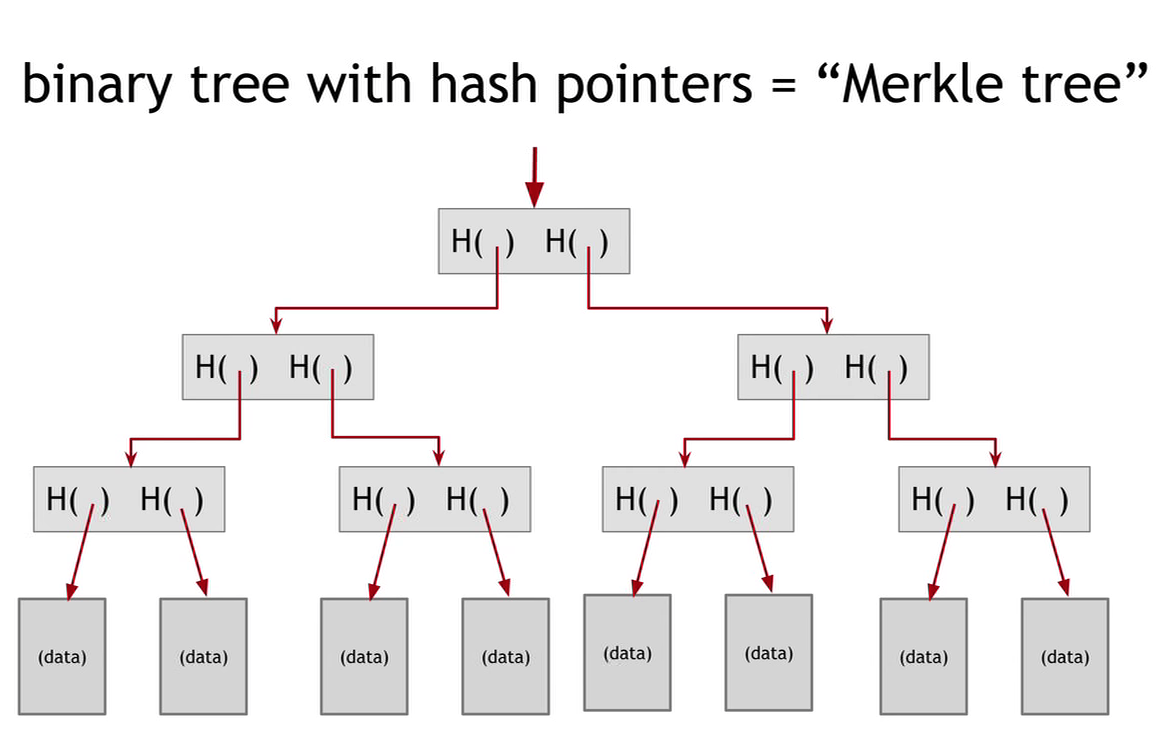
可以在 O(log n) 的时间内验证梅克尔树的隶属关系。
可以在 O(log n) 的时间内验证经过已经规则排序之后的梅克尔树的非隶属关系。
1.3 数字签名 (Digital Signatures)
签名目的
-
只有你能签,但别人都能验证。
-
签名只能用于指定文档,不能通过剪切复制到其他文档。
签名方案步骤
- 生成 sk 和 pk,sk 用于加密签名,pk 用于公开验证。如下:
- 将 sk 和 message 作为输入,生成电子签名(signature):
- 将 signature 和 pk 公布,让他人可验证。
方案要求
-
加密算法需要保证其的随机性。
-
信息大小限制。通过对信息的哈希值进行加密,可以间接实现对信息的签名。当然也可以对信息的哈希指针进行签名,哈希指针可以保护对其的整个结构,包括哈希指针和其指向的整个区块链。
椭圆数字签名算法
比特币使用椭圆数字签名算法,即 Elliptic Curve Digital Signature Algorithm (ECDSA),虽然怪异(不良随机可能导致密钥泄露),但是这是由中本聪在比特币系统早期选定。因此使用 ECDSA 时,需要确保良好的随机性来源。
1.4 公钥作为身份 (Public Keys as Identities)
公钥 public key 可以代表私钥 private key 的公众身份,而 private key 则是此人身份真实的内涵。可以通过多组 private key/public key 来进行获取多个身份,保证隐匿性。
在比特币交易时使用同一个地址,则可能泄露身份。
1.5 简单的加密货币
高飞币 (GoofyCoin)
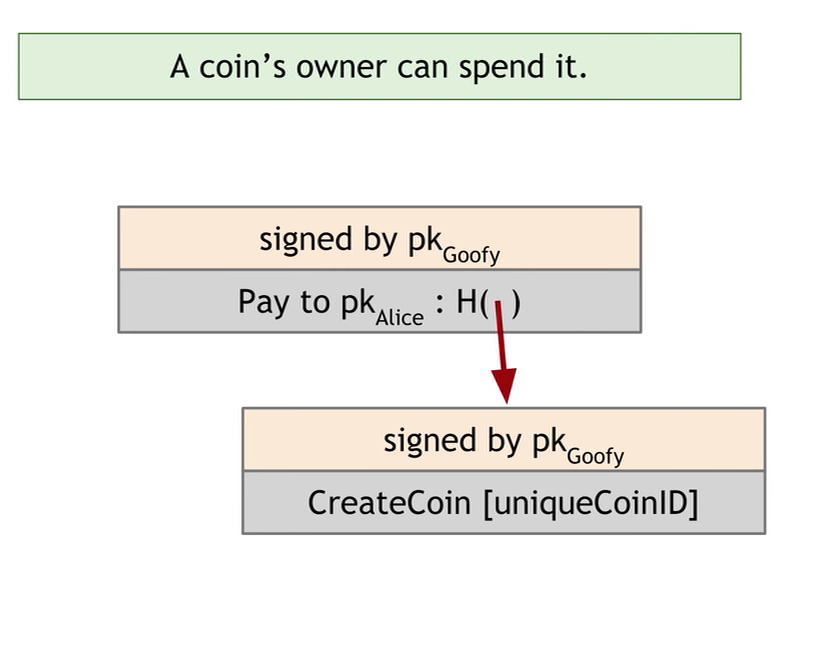
第一个规则:Goofy 可随时创建新币。
Goofy 创造一枚唯一编号的货币,使用私钥对其进行数字签名。其他人都可以验证签名的有效性。
第二个规则:拥有此币的人可以转给他人。
这个过程需要创造一个声明,表示“将此币支付给 Alice”:“此币”即哈希指针,指向前一个区块 block,也就是“Goofy 创造钱币”;“Alice”即身份,也就是公钥。Goofy 会将这个信息和哈希指针进行签名,用来证明这个币的确已经转给了 Alice。
Alice 也可以用同样的方式新增一个 block,对信息和哈希指针签名,将此币转给 Bob。
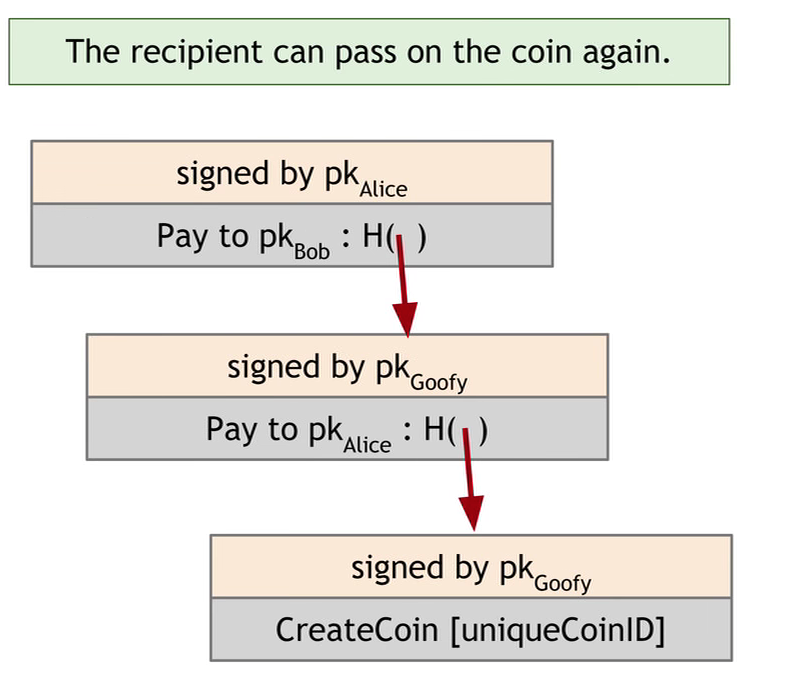
这样会有双重支付 (Double-spending attack) 的问题,Alice 可以同时新增另一个 block,声明将此币转给了 Chuck。
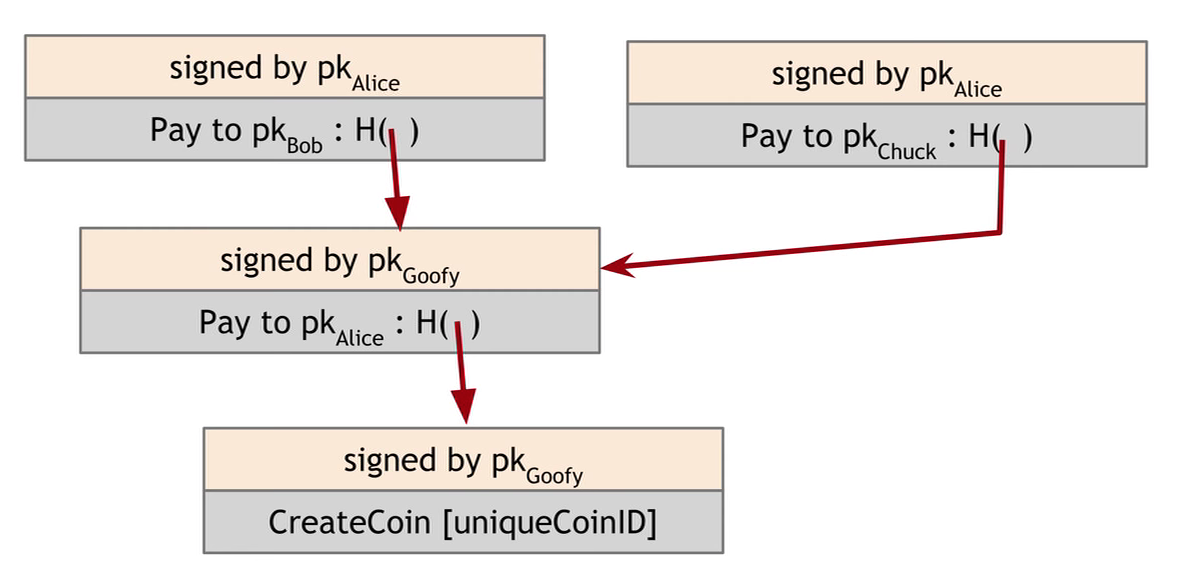
守财奴币 (ScroogeCoin)
守财奴币新增了标识交易顺序的 id,守财奴 Scrooge 将公布所有的交易的记录。通过区块链的数据结构,只需要两个人通过对比各自最后获取到的哈希指针便可以验证守财奴有没有篡改过交易记录。
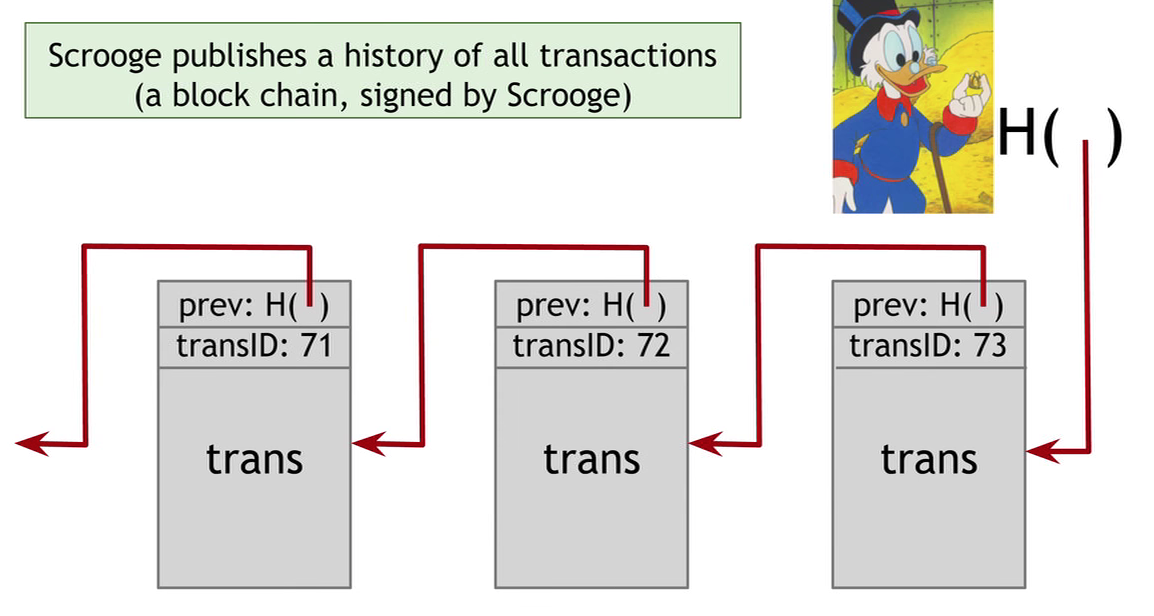
守财奴币中的交易种类:
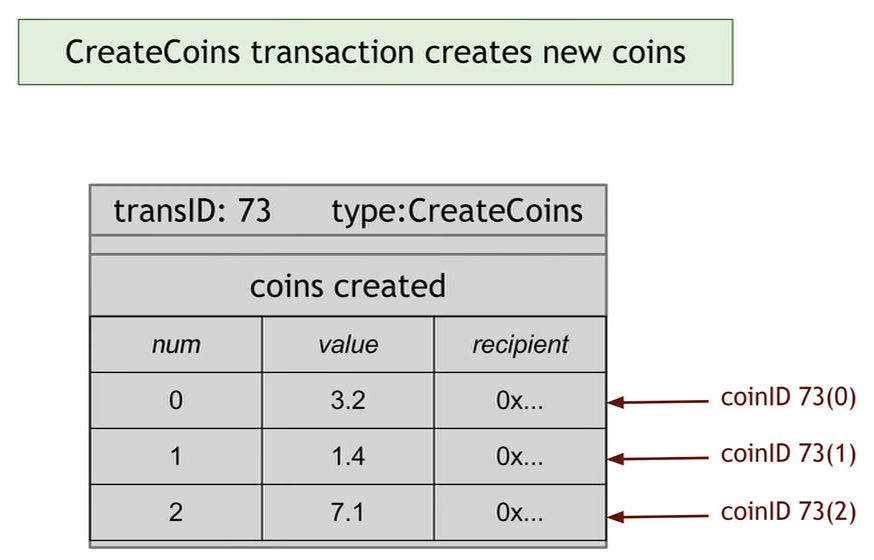
1.造币,CreateCoins。在所有人都认定守财奴造币是合法的这一前提下,每个造币交易可以创建多个币。每个币都会有序号。
2.支付,PayCoins。过程为,消耗币的同时产生同价值的币,执行支付的人会对其进行签名,表明同意此交易。每次支付都需要一次签名。
满足以下规则被认定交易有效:
-
被消耗的币为之前造币交易中创造出来的币。
-
被消耗的币之前没有被交易过。
-
产生币的总量等于消耗币的总量。
-
被消耗的币被其所有者签名认同。
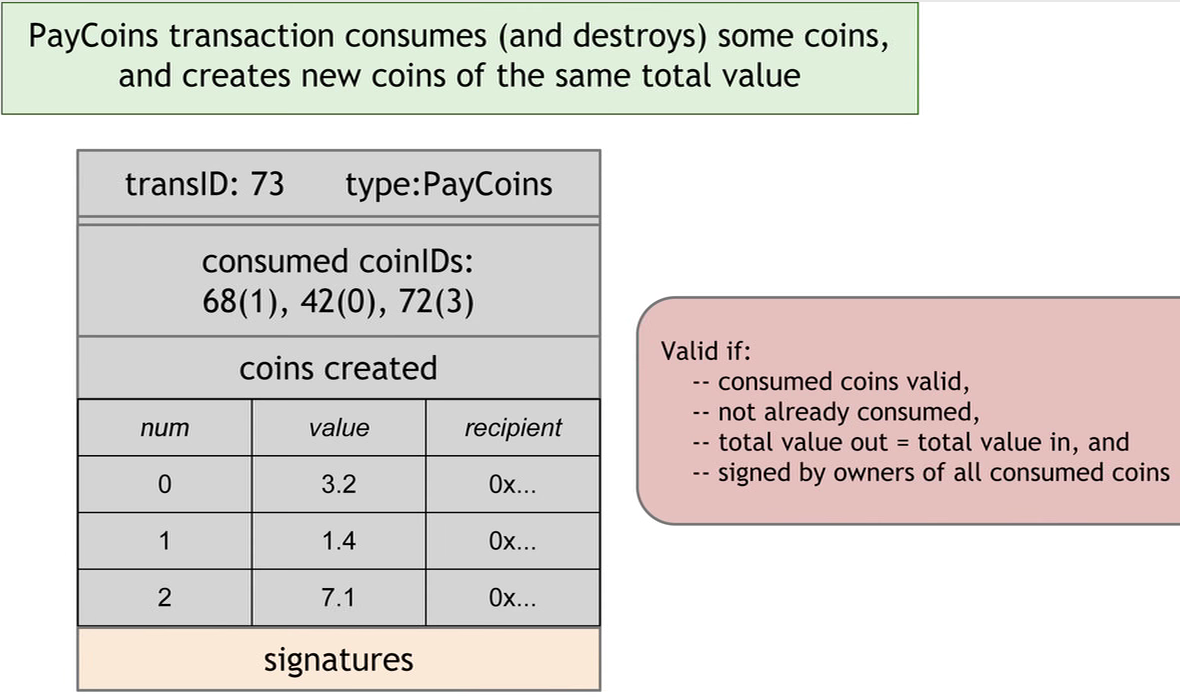
注意此过程中币是不可变的,只能被消耗和创造。支付的过程是消耗旧币,创造新币,声明他人拥有新币的过程。这个特性是理解比特币的支付的关键。
之后,守财奴会认定交易有效,会将交易添加到区块链并公布。
这样会使得守财奴权力过大,出现中心化的问题。
下一章节会讨论如何实现去中心化。