关于NSDictionary
11 Jul 2016
前言
聊得时候遇到这么个问题:实现上千对象的存储到字典(OC下就是NSDictionary)时,如果出现效率低下的问题,可能是什么原因?一脸懵逼啊,后来才知道重点在于NSDictionary的实现(hash算法及冲突的解决)。
hash算法及冲突的解决
NSDictionary(字典)是使用 hash表来实现key和value之间的映射和存储的。hash基本思想是:首先在元素的关键字 k 和元素的存储位置 p 之间建立一个对应关系 f ,使得 p=f(k) ,f 称为哈希函数 。创建哈希表时,把关键字为 k 的元素 直接存入地址为 f(k) 的单元 ;以后当查找关键字为 k 的元素时,再利用哈希函数计算出该元素的存储位置 p=f(k) ,从而达到按关键字直接存取元素的目的。当关键字集合很大时,关键字值不同的元素可能会映象到哈希表的同一地址上 ,即 k1 ≠ k2 ,但 H(k1) = H(k2),这种现象称为冲突,此时称 k1 和 k2 为同义词。实际中,冲突是不可避免的,只能通过改进哈希函数的性能来减少冲突。
综上所述,哈希法主要包括以下两方面的内容: 1.如何构造哈希函数 2.如何处理冲突。
哈希函数的构造方法
构造哈希函数的原则是:1.函数本身便于计算;2.计算出来的地址分布均匀,即对任一关键字k,f(k) 对应不同地址的概率相等,目的是尽可能减少冲突。 下面介绍构造哈希函数常用的五种方法。
1.数字分析法
如果事先知道关键字集合,并且每个关键字的位数比哈希表的地址码位数多时,可以从关键字中选出分布较均匀的若干位,构成哈希地址。例如,有80个记录,关键字为8位十进制整数d1d2d3…d7d8,如哈希表长取100,则哈希表的地址空间为:00~99。假设经过分析,各关键字中 d4和d7的取值分布较均匀,则哈希函数为:h(key)=h(d1d2d3…d7d8)=d4d7。例如,h(81346532)=43,h(81301367)=06。相反,假设经过分析,各关键字中 d1和d8的取值分布极不均匀, d1 都等于5,d8 都等于2,此时,如果哈希函数为:h(key)=h(d1d2d3…d7d8)=d1d8,则所有关键字的地址码都是52,显然不可取。
2.平方取中法
当无法确定关键字中哪几位分布较均匀时,可以先求出关键字的平方值,然后按需要取平方值的中间几位作为哈希地址。这是因为:平方后中间几位和关键字中每一位都相关,故不同关键字会以较高的概率产生不同的哈希地址。 例:我们把英文字母在字母表中的位置序号作为该英文字母的内部编码。例如K的内部编码为11,E的内部编码为05,Y的内部编码为25,A的内部编码为01, B的内部编码为02。由此组成关键字“KEYA”的内部代码为11052501,同理我们可以得到关键字“KYAB”、“AKEY”、“BKEY”的内部编码。之后对关键字进行平方运算后,取出第7到第9位作为该关键字哈希地址,如图:
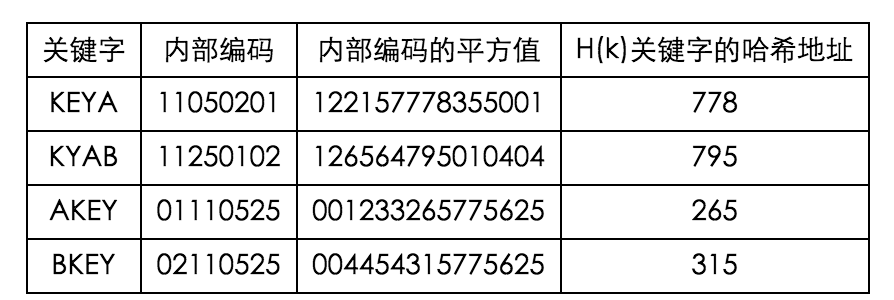
3.分段叠加法 这种方法是按哈希表地址位数将关键字分成位数相等的几部分(最后一部分可以较短),然后将这几部分相加,舍弃最高进位后的结果就是该关键字的哈希地址。具体方法有折叠法与移位法。移位法是将分割后的每部分低位对齐相加,折叠法是从一端向另一端沿分割界来回折叠(奇数段为正序,偶数段为倒序),然后将各段相加。例如:key=12360324711202065,哈希表长度为1000,则应把关键字分成3位一段,在此舍去最低的两位65,分别进行移位叠加和折叠叠加,求得哈希地址为105和907,如图:
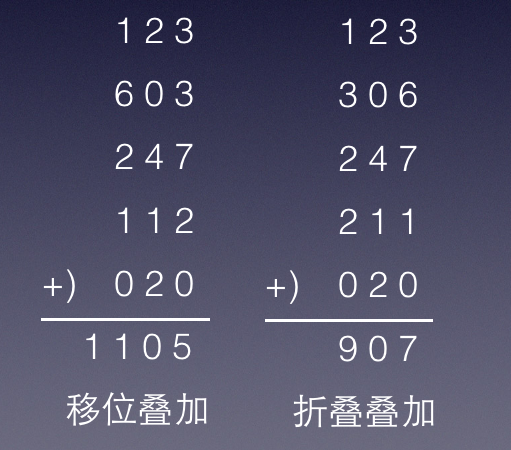
4.除留余数法
假设哈希表长为m,p为小于等于m的最大素数,则哈希函数为 h(k)= k%p ,其中%为模p取余运算。
例如,已知待散列元素为(18,75,60,43,54,90,46),表长m=10,p=7,则有
h(18)=18 % 7=4 h(75)=75 % 7=5 h(60)=60 % 7=4
h(43)=43 % 7=1 h(54)=54 % 7=5 h(90)=90 % 7=6
h(46)=46 % 7=4
此时冲突较多。为减少冲突,可取较大的m值和p值,如m=p=13,结果如下:
h(18)=18 % 13=5 h(75)=75 % 13=10 h(60)=60 % 13=8
h(43)=43 % 13=4 h(54)=54 % 13=2 h(90)=90 % 13=12
h(46)=46 % 13=7
此时没有冲突,如图:

5.伪随机数法 采用一个伪随机函数做哈希函数,即h(key)=random(key)。 在实际应用中,应根据具体情况,灵活采用不同的方法,并用实际数据测试它的性能,以便做出正确判定。通常应考虑以下五个因素 :
- 计算哈希函数所需时间 (简单)。
- 关键字的长度。
- 哈希表大小。
- 关键字分布情况。
- 记录查找频率
处理冲突
通过构造性能良好的哈希函数,可以减少冲突,但一般不可能完全避免冲突,因此解决冲突是哈希法的另一个关键问题。创建哈希表和查找哈希表都会遇到冲突,两种情况下解决冲突的方法应该一致。下面以创建哈希表为例,说明解决冲突的方法。常用的解决冲突方法有以下四种:
1.开放定址法。这种方法也称再散列法,其基本思想是:当关键字 key 的哈希地址 p = H(key) 出现冲突时,以 p 为基础(不是为key哦),产生另一个哈希地址 p1 ,如果 p1 仍然冲突,再以 p1 为基础,产生另一个哈希地址 p2…,直到找出一个不冲突的哈希地址 pi,将相应元素存入其中。这种方法有一个通用的再散列函数形式:
Hi=(H(key)+di)% m i=1,2,…,n
其中H(key)为哈希函数,m 为表长,di称为增量序列。增量序列的取值方式不同,相应的再散列方式也不同。主要有以下三种:
- 线性探测再散列 ` di=1,2,3,…,m-1`
这种方法的特点是:冲突发生时,顺序查看表中下一单元,直到找出一个空单元或查遍全表。
- 二次探测再散列
di=12,-12,22,-22,…,k2,-k2 (k<=m/2)
这种方法的特点是:冲突发生时,在表的左右进行跳跃式探测,比较灵活。
- 伪随机探测再散列
di=伪随机数序列
具体实现时,应建立一个伪随机数发生器(如i=(i+p)%m),并给定一个随机数做起点。
例如,已知哈希表长度m=11,哈希函数为:H(key) = key%11,则H(47)=3,H(26)=4,H(60)=5,假设下一个关键字为69,则H(69)=3,与47冲突。
如果用线性探测再散列处理冲突,下一个哈希地址为H1=(3 + 1)% 11 = 4,仍然冲突,再找下一个哈希地址为H2=(3 + 2)% 11 = 5,还是冲突,继续找下一个哈希地址为H3=(3 + 3)% 11 = 6,此时不再冲突,将69填入5号单元,如图:

如果用二次探测再散列处理冲突,下一个哈希地址为H1=(3 + 12)% 11 = 4,仍然冲突,再找下一个哈希地址为H2=(3 - 12)% 11 = 2,此时不再冲突,将69填入2号单元,如图:

如果用伪随机探测再散列处理冲突,且伪随机数序列为:2,5,9,……..,则下一个哈希地址为H1=(3 + 2)% 11 = 5,仍然冲突,再找下一个哈希地址为H2=(3 + 5)% 11 = 8,此时不再冲突,将69填入8号单元,如图:

从上述例子可以看出,线性探测再散列容易产生“二次聚集”,即在处理同义词的冲突时又导致非同义词的冲突。例如,当表中i, i+1 ,i+2三个单元已满时,下一个哈希地址为i, 或i+1 ,或i+2,或i+3的元素,都将填入i+3这同一个单元,而这四个元素并非同义词。线性探测再散列的优点是:只要哈希表不满,就一定能找到一个不冲突的哈希地址,而二次探测再散列和伪随机探测再散列则不一定。
2.再哈希法。这种方法是同时构造多个不同的哈希函数:Hi = RH1(key) i=1 , 2 , … , k。当哈希地址 Hi = RH1(key) 发生冲突时,再计算 Hi = RH2(key)……,直到冲突不再产生。这种方法不易产生聚集,但增加了计算时间。
3.链地址法。这种方法的基本思想是将所有哈希地址为 i 的元素构成一个称为同义词链的单链表 ,并将单链表的头指针存在哈希表的第 i 个单元中,因而查找、插入和删除主要在同义词链中进行。链地址法适用于经常进行插入和删除的情况。 例如,已知一组关键字(32,40,36,53,16,46,71,27,42,24,49,64),哈希表长度为13,哈希函数为:H(key)= key % 13,则用链地址法处理冲突的结果。
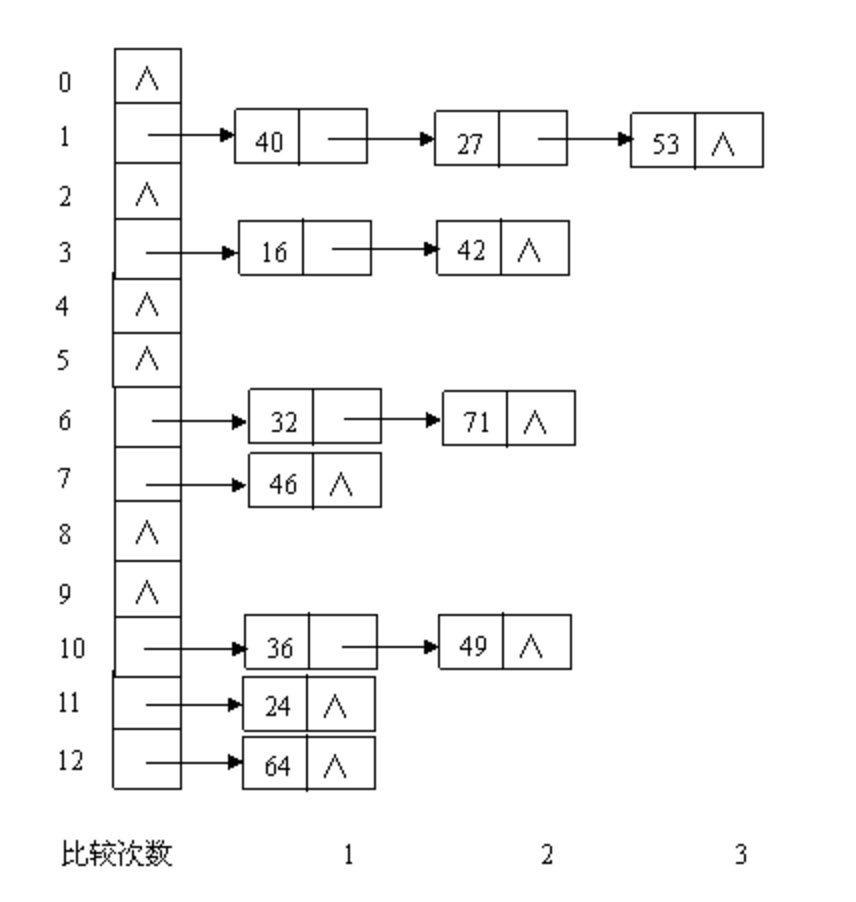
OC的hash
苹果OC源代码的hash结构就是采用这种各大数据结构体教材中都会讲的类似于链地址的方式解决冲突的。不过它的链地址不是一个链表,而是一个数组结构,而且当出现冲突的时候,它通过释放原来的数组结构,并进行分配大一个数组结构来存放新的元素的。它的劣势很明显,如果冲突比较多会频繁的alloc和free,它的优势是不用二级指针的指向来找到元素,为了进一步优化,它对于一个和两个元素采用了oneOrMany的 union 结构,这样对一个的元素进行hashGet会减少一次二级指针的获取操作,这应该是预估了冲突一般情况下都很少发生才这样做的。整个Hash结构是一个大数组,数组的基地址是buckets。每一个bucket可以看成是一个小数组,它存储着具有相同hash值的冲突列表。
到这里也就可以推断出,如果在NSDictionary存取时出现效率低下的情况,那么很可能是: 1.频繁的扩容 2.冲突过多
更多的实现细节可以参考以下链接: